BOJ 2261:: 가장 가까운 두 점

2016년 11월 22일

흔히 closest pair problem이라고 부르는 아주 유명한 문제입니다.

모든 쌍 다 고려하기

점 두 개를 고르는 방법은 $n(n-1)/2$가지니까, 각각에 대해 거리를 재고 그 중에 최솟값을 구하면 $O(n^2)$입니다.

분할 정복

$y$축과 나란하게 직선을 그어서 평면을 둘로 나눕시다. 모든 점을 $x$ 좌표 기준으로 정렬한 다음 $n/2$번째와 $n/2+1$번째 점의 $x$ 좌표 평균을 기준 직선으로 잡겠습니다.

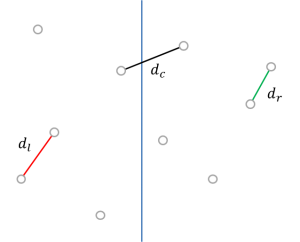
그러면 문제가 총 세 가지 경우로 나뉩니다.

  1. 두 점 모두 왼쪽에 속할 경우
  2. 두 점 모두 오른쪽에 속할 경우
  3. 서로 다른 쪽에 속할 경우

각 경우에 대해서 최솟값을 구한 다음 세 가지 중에서 제일 작은 게 문제의 최종 정답이 되겠죠. 위 그림에서 각각을 $d_l$, $d_r$, $d_c$로 나타냈습니다. 1번과 2번의 최솟값은 재귀적으로 답을 구할 수 있습니다. 3번은 왼쪽에 $n/2$개, 오른쪽에 $n/2$개씩 있으니까 양쪽에서 하나씩 뽑으면 총 $n^2/4$가지 경우가 있고, 모든 경우에 대해 다 길이를 계산한 다음 그 최솟값을 찾읍시다. 그래서 시간복잡도 $T(n)$은

\[ T(n) = 2T(n/2) + O(n^2) \]

을 만족하고, 마스터 정리를 쓰면 $T(n) = O(n^2)$임을 알 수 있습니다.

시간복잡도 줄이기

아쉽지만 시간 복잡도가 전혀 줄어들지 않았습니다. 3번 최솟값을 구하는 데 $O(n^2)$씩이나 걸리기 때문이죠. 이걸 줄이려면 절대 답이 될 거 같지 않은 쌍을 가지치기하고 남은 쌍에 대해서만 계산해야 합니다. 일단 1번의 최솟값과 2번의 최솟값 중 더 작은 쪽을 d라고 합시다. 즉, $d=\min(d_l,d_r)$입니다. 이제 3번 중에서 거리가 $d$보다 큰 쌍은 비교하지 않으면 됩니다.

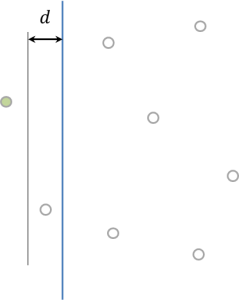
위 그림에서 파란색 선은 좌우를 나누는 기준선입니다. 그리고 기준선까지 거리가 $d$보다 큰 초록색 점을 생각하면 이 초록색 점은 오른쪽에 있는 어떤 점과 비교해봐도 당장 $x$ 좌표부터가 $d$보다 크게 차이나니 초록색 점을 포함하는 쌍은 절대로 거리가 $d$이하일 리 없습니다. 따라서 초록색 점은 3번 계산에서 무시해도 괜찮습니다. 즉, 기준선을 중심으로 좌우 거리 $d$ 이내에 들어오는 점끼리만 비교하면 됩니다.그렇다고 문제가 해결된 건 아니죠. 만약 모든 점이 그 영역 안에 들어오면 이 방법도 쓸모가 없습니다.

기준선을 중심으로 거리가 $d$이내인 영역에 있는 점들을 $y$좌표 기준으로 정렬해봅시다. 영역 내에서 기준선 왼쪽과 오른쪽은 구분하지 않겠습니다. 그리고 제일 아래에 있는 점부터 시작해서 각 점을 자기보다 더 위에 있는 점($y$좌표가 자기와 같거나 더 큰 점)이랑만 비교한다고 합시다. 중복을 피하기 위해서죠. 근데 점이 100개가 있다고 할 때 제일 아래에 있는 점을 나머지 99개 모두와 비교할 필요는 전혀 없습니다. 상식적으로 이렇게 점이 많으면 일단 제일 위 점이랑은 거리가 아무리 그래도 $d$보단 멀겠죠.

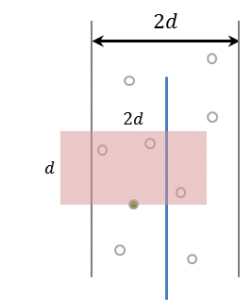
초록색 점을 봅시다. 초록색 점을 기준으로 두고 자기보다 위에 있는 점만 비교한다고 하면 우리가 비교해야 할 나머지 한쪽 점은 분명 저 빨간색 직사각형 내부에 있는 점들일 겁니다. 저 밖의 점들은 $y$좌표부터가 $d$ 이상 차이나므로 절대 답이 될 수 없습니다. 결론적으로 $y$좌표 기준으로 정렬한 뒤 각 점을 자기보다 $y$좌표가 같거나 높은 것들을 비교하다가 $y$좌표 차가 $d$ 이상이 되면 그 점에 대한 비교를 끝내면 됩니다. 그렇다면 문제는 비교가 최대 몇 번이냐는 건데, 절대 7번을 넘지 않습니다. (증명)

이제는 3번의 최솟값을 계산하는 데 $O(n\log n)$이 걸리니까 확실히 많이 줄어들죠.

  1. $y$좌표 기준 정렬: $O(n\log n)$
  2. 최대 $n$개의 점에 대해 각 점을 최대 점 7개와 비교: $O(n)$

따라서 시간복잡도는

\[ T(n) = 2T(n/2) + O(n\log n) \]

을 만족하고 역시 마스터 정리를 쓰면 $T(n) = O(n\log^2n)$이 됩니다. 

#include<bits/stdc++.h>

using namespace std;

struct Point {
    int x, y;
};

int dist(Point &p, Point &q) {
    return (p.x-q.x)*(p.x-q.x)+(p.y-q.y)*(p.y-q.y);
}

struct Comp {
    bool comp_in_x;
    Comp(bool b) : comp_in_x(b) {}
    bool operator()(Point &p, Point &q) {
        return (this->comp_in_x? p.x < q.x : p.y < q.y);
    }
};


int closest_pair(vector<Point>::iterator it, int n) {
    if (n == 2)
        return dist(it[0], it[1]);
    if (n == 3)
        return min({dist(it[0], it[1]), dist(it[1], it[2]), dist(it[2], it[0])});

    int line = (it[n/2 - 1].x + it[n/2].x) / 2;
    int d = min(closest_pair(it, n/2), closest_pair(it + n/2, n - n/2));

    vector<Point> mid;
    mid.reserve(n);

    for (int i = 0; i < n; i++) {
        int t = line - it[i].x;
        if (t*t < d)
            mid.push_back(it[i]);
    }

    sort(mid.begin(), mid.end(), Comp(false));

    int mid_sz = mid.size();
    for (int i = 0; i < mid_sz - 1; i++)
        for (int j = i + 1; j < mid_sz && (mid[j].y - mid[i].y)*(mid[j].y - mid[i].y) < d; j++)
            d = min(d, dist(mid[i], mid[j]));

    return d;
}


int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n;
    cin >> n;

    vector<Point> points(n);
    for (auto it = points.begin(); it != points.end(); it++)
        cin >> it->x >> it->y;

    sort(points.begin(), points.end(), Comp(true));

    cout << closest_pair(points.begin(), n);

    return 0;
}

다른 알고리즘

여기서는 3번에서 일일이 정렬을 했기 때문에 $O(n\log^2n)$이라는 시간복잡도가 나왔지만, 병합 정렬의 아이디어를 이용해서 정렬을 $O(n)$에 하여 $O(n\log n)$에 할 수도 있습니다. 또한, 라인 스위핑 기법을 사용하여도 $O(n\log n)$을 얻을 수 있습니다.

PS