BOJ 1006:: 습격자 초라기

아주 유명하고 어려운 문제입니다. 문제 목록 첫 페이지 최상단에 뜨는 문제라 순서대로 문제 푸는 초보자들을 좌절시키는 문제죠.

당연하게도 원형으로 된 배열이 주어지면 문제가 매우 어렵기 때문에, 건물이 $N\times2$짜리 직사각형인 경우를 먼저 풀어봅시다. 이렇게 되면 원타곤이 아니라 직타곤이라고 불러야 할까요…? 편의상 건물의 위쪽을 1행, 아래쪽을 2행이라 하고 왼쪽부터 차례로 0열부터 N-1열까지로 부르겠습니다.

먼저 동적 계획법을 사용하기 위해 세 배열을 다음과 같이 정의합니다.

그림으로 나타내면 아래와 같습니다. 회색이 특수소대로 채워진 구역, 흰색이 아직 채우지 않은 구역입니다.

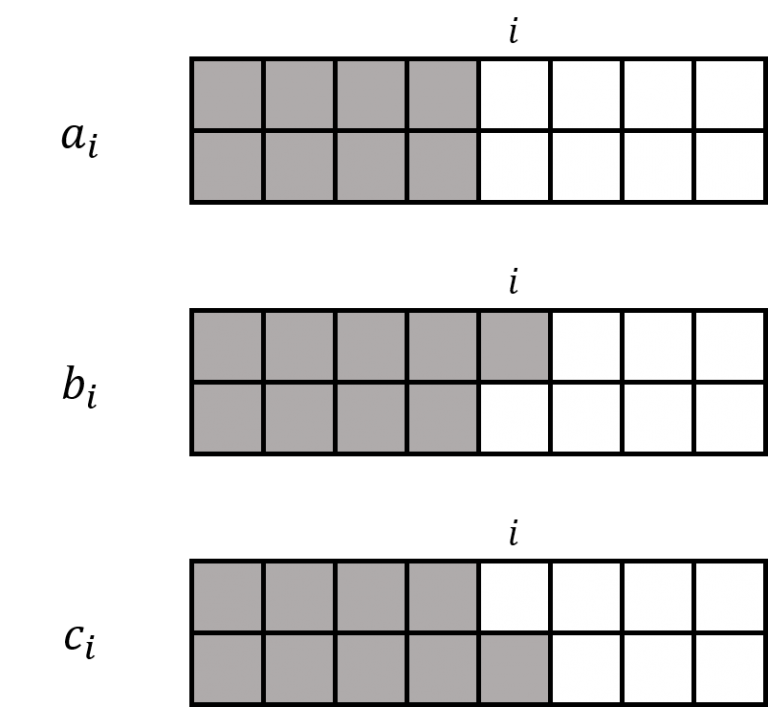
이제 점화식을 구합시다. 1행과 2행 모두 $i$열까지 채우는 방법은 네 가지가 있습니다.

  1. 1행과 2행 모두 $i-1$열까지 채우고 1행 $i$열과 2행 $i$열에 특수소대 하나를 채움
  2. 1행과 2행 모두 $i-2$열까지 채우고 1행 $i-1$열과 1행 $i$열에 특수소대 하나, 2행 $i-1$열과 2행 $i$열에 하나를 채움
  3. 1행은 $i$열까지, 2행은 $i-1$열까지 채우고 2행 $i$열에 특수소대 하나를 채움
  4. 1행은 $i-1$열까지, 2행은 $i$열까지 채우고 1행 $i$열에 특수소대 하나를 채움

단, 첫 번째와 두 번째는 두 구역에 걸쳐 특수소대 하나를 배치하므로 두 구역에 있는 적의 수가 합쳐서 $W$보다 작은 경우에만 가능합니다. 정리하자면,

\begin{align*} & a_{i+1} \leftarrow \min(b_i+1, c_i+1) \\ & \textbf{if }\ e_{1,i}+e_{2,i} \le W \\ & \qquad a_{i+1} \leftarrow \min(a_{i+1}, a_i+1) \\ & \textbf{if }\ i > 0 \ \textbf{ and }\ e_{1,i-1} + e_{1,i} \le W \ \textbf{ and }\ e_{2,i-1} + e_{2,i} \le W \\ & \qquad a_{i+1} \leftarrow \min(a_{i+1}, a_{i-1}+2) \end{align*}

여기서 $e_{i,j}$는 $i$행 $j$열에 있는 적의 수입니다. 한편 1행은 $i+1$열까지 채우고 2행은 $i$열까지 채우는 방법은 두 가지가 있습니다.

  1. 1행과 2행 모두 $i$열까지 채우고 1행 $i+1$열에 특수소대 하나를 채움
  2. 1행은 $i-1$열, 2행은 $i$열까지 채우고 1행 $i$열과 1행 $i+1$열에 특수소대 하나를 채움

따라서

\begin{align*} & b_{i+1} \leftarrow a_{i+1}+1 \\ & \textbf{if }\ e_{1,i}+e_{1,i+1} \le W \\ & \qquad b_{i+1} \leftarrow \min(b_{i+1}, c_i+1) \end{align*}

마지막으로 1행은 $i$열까지, 2행은 $i+1$열까지 채우는 방법을 위와 비슷하게 계산하면 $c_{i+1}$에 대한 점화식을 구할 수 있습니다.

\begin{align*} & c_{i+1} \leftarrow a_{i+1}+1 \\ & \textbf{if }\ e_{2,i}+e_{2,i+1} \le W \\ & \qquad c_{i+1} \leftarrow \min(c_{i+1}, b_i+1) \end{align*}

점화식을 구한 걸로 끝이 아니라 초기값도 구해야죠. $a_0$는 1행과 2행 모두 -1열까지 채우라는 의미인데 채울 필요가 없으니 0입니다. $b_0$와 $c_0$는 둘 다 1이고요. 최종 정답은 $a_N$입니다.

이제 다시 원형으로 돌아옵시다. 앞에서 푼 선형 문제는 1번 구역과 $N$번 구역에 걸쳐 특수소대를 채우지 않고 $N+1$번 구역과 $2N$번 구역에 걸쳐 특수소대를 채우지 않는 경우와 동일합니다. 만약 1번 구역과 $N$번 구역에 걸쳐 특수소대를 채우고 $N+1$번 구역과 $2N$번 구역에 걸쳐 특수소대를 채우지 않으면 초기 조건이 달라져야 합니다. 이때는 $N\times2$ 직사각형 건물에서 1행 0열과 1행 $N-1$행이 없어졌다고 생각하면 됩니다. 그럼 $a_1$은 1, $b_1$은 2, $c_1$은 $e_{2,0}+e_{2,1}\le W$이면 1, 아니면 2가 초기 조건이 되고, 최종 정답은 $c_{N-1}+1$입니다. 마지막에 1을 더하는 이유는 1행 0열과 1행 $N-1$행에 배치된 특수소대가 있기 때문이죠.

1번과 $N$번 구역에 걸쳐 특수소대를 채우지 않고 $N+1$번과 $2N$번 구역에 걸쳐 특수소대를 채우면 위와 정확히 반대 상황이며, 양쪽 다 걸쳐 채운다고 하면 $a_1$은 0, $b_1$과 $c_1$은 1이고 최종 정답은 $a_{N-1}+2$입니다.

마지막으로, $N$이 1일 때 예외 처리가 필요합니다. 

#include<bits/stdc++.h>

using namespace std;

int n, w, res;
int e[10000][2], a[10001], b[10000], c[10000];

void solve(int start) {
    for (int i = start; i < n; i++) {
        a[i+1] = min(b[i] + 1, c[i] + 1);
        if (e[i][0] + e[i][1] <= w)
            a[i+1] = min(a[i+1], a[i] + 1);
        if (i > 0 && e[i-1][0] + e[i][0] <= w && e[i-1][1] + e[i][1] <= w)
            a[i+1] = min(a[i+1], a[i-1] + 2);
        if (i < n-1) {
            b[i+1] = a[i+1] + 1;
            if (e[i][0] + e[i+1][0] <= w)
                b[i+1] = min(b[i+1], c[i] + 1);
            c[i+1] = a[i+1] + 1;
            if (e[i][1] + e[i+1][1] <= w)
                c[i+1] = min(c[i+1], b[i] + 1);
        }
    }
}

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int t;

    cin >> t;
    while (t--) {
        cin >> n >> w;
        res = 30000;

        for (int i = 0; i < n; i++)
            cin >> e[i][0];
        for (int i = 0; i < n; i++)
            cin >> e[i][1];

        a[0] = 0;
        b[0] = c[0] = 1;
        solve(0);
        res = min(res, a[n]);

        if (n > 1 && e[0][0] + e[n-1][0] <= w) {
            a[1] = 1;
            b[1] = 2;
            c[1] = e[0][1] + e[1][1] <= w? 1 : 2;
            solve(1);
            res = min(res, c[n-1] + 1);
        }

        if (n > 1 && e[0][1] + e[n-1][1] <= w) {
            a[1] = 1;
            b[1] = e[0][0] + e[1][0] <= w? 1 : 2;
            c[1] = 2;
            solve(1);
            res = min(res, b[n-1] + 1);
        }

        if (n > 1 && e[0][0] + e[n-1][0] <= w && e[0][1] + e[n-1][1] <= w) {
            a[1] = 0;
            b[1] = c[1] = 1;
            solve(1);
            res = min(res, a[n-1] + 2);
        }

        cout << res << '\n';
    }

    return 0;
}
PS