0-1 BFS

그래프 변의 가중치가 모두 0 아니면 1인 그래프에서는 BFS와 다익스트라를 합친 듯한 느낌의 알고리즘인 0-1 BFS를 써서 최단 경로를 구할 수 있습니다. 알고리즘은 간단합니다. 꼭짓점의 집합을 $V$, 출발점을 $s$, 각 꼭짓점까지 최단 거리를 저장하는 배열을 $dist$라 할 때 의사코드는 아래와 같습니다.

\begin{align*} & \textbf{for } \text{each vertex } v \in V \\ & \qquad dist[v] \leftarrow \infty \\ & dist[s] \leftarrow 0 \\ & \\ & Q \leftarrow \emptyset \\ & \text{PushBack}(Q, s) \\ & \textbf{while } Q \neq \emptyset \\ & \qquad u \leftarrow \text{PopFront}(Q) \\ & \qquad \textbf{for } \text{each edge } e \text{ adjacent to } u \\ & \qquad\qquad v \leftarrow \text{the opponent vertex of } u \text{ in } e \\ & \qquad\qquad w \leftarrow \text{the weight of } e \\ & \qquad\qquad \textbf{if } dist[v] > dist[u] + w \\ & \qquad\qquad\qquad dist[v] \leftarrow dist[u] + w \\ & \qquad\qquad\qquad \textbf{if } w = 0 \\ & \qquad\qquad\qquad\qquad \text{PushFront}(Q, v) \\ & \qquad\qquad\qquad \textbf{else} \\ & \qquad\qquad\qquad\qquad \text{PushBack}(Q, v) \end{align*}

$Q$의 앞과 뒤 모두에 원소를 넣을 수 있어야 하기 때문에 큐를 쓰는 BFS와 달리 $Q$가 덱(deque)이어야 합니다.

응용

BOJ 2636:: 치즈

흔히 다익스트라로 많이 풀지만 0-1 BFS로도 풀 수 있습니다. 먼저 모든 칸을 그래프의 꼭짓점으로 두고, 인접한 칸 사이에 변을 놓습니다. 변의 가중치는 치즈가 있는 칸으로 가면 1, 없는 칸으로 가면 0입니다.

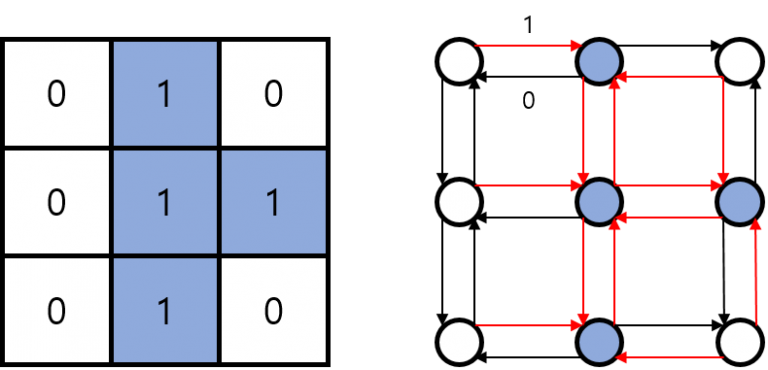
이때 제일 왼쪽 위에서 출발하여 치즈가 있는 어떤 칸까지 최단 거리를 구하면 그것이 그 칸이 녹는 데 걸리는 시간입니다. 정답은 최단 거리의 최댓값과 그 값을 갖는 치즈의 개수가 되겠죠.



#include<bits/stdc++.h>

using namespace std;
using ll = long long;
using ull = unsigned long long;
using Pint = pair<int, int>;
using Tint = tuple<int, int, int>;

int r, c;
int board[100][100];
int dist[100][100];

const int adj[4][2] = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
const int INF = 1000000000;

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> r >> c;
    for (int i = 0; i < r; i++)
        for (int j = 0; j < c; j++)
            cin >> board[i][j];

    fill(&dist[0][0], &dist[0][0] + 10000, INF);
    dist[0][0] = 0;

    deque<Pint> q{{0, 0}};

    while (!q.empty()) {
        auto [cr, cc] = q.front();
        q.pop_front();

        for (int k = 0; k < 4; k++) {
            int nr = cr + adj[k][0], nc = cc + adj[k][1];
            if (nr < 0 || nr >= r || nc < 0 || nc >= c)
                continue;

            int w = board[nr][nc];
            if (dist[nr][nc] > dist[cr][cc] + w) {
                dist[nr][nc] = dist[cr][cc] + w;
                if (w == 0)
                    q.push_front({nr, nc});
                else
                    q.push_back({nr, nc});
            }
        }
    }

    int max_dist = 0, cnt = 0;
    for (int i = 0; i < r; i++)
        for (int j = 0; j < c; j++)
            max_dist = max(max_dist, dist[i][j]);
    for (int i = 0; i < r; i++)
        for (int j = 0; j < c; j++)
            if (board[i][j] == 1 && dist[i][j] == max_dist)
                cnt++;

    cout << max_dist << '\n' << cnt;

    return 0;
}

BOJ 6087:: 레이저 통신

모든 칸을 가로와 세로 두 꼭짓점으로 나눠서 가로 꼭짓점은 가로로 이웃한 다른 가로 꼭짓점과 가중치 0인 변으로 이어주고, 세로 꼭짓점은 세로로 이웃한 세로 꼭짓점과 가중치 0으로 이어주고, 같은 칸의 두 꼭짓점끼리는 가중치 1인 변으로 이어서 최단 거리를 구하면 정답입니다.



#include<bits/stdc++.h>

using namespace std;
using ll = long long;
using ull = unsigned long long;
using Pint = pair<int, int>;
using Tint = tuple<int, int, int>;

int w, h;
char board[100][101];

vector<Pint> site;
int sr, sc, er, ec;

int dist[100][100][2];

constexpr int adj[4][2] = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
constexpr int INF = 1000000000;

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> w >> h;
    for (int i = 0; i < h; i++) {
        cin >> board[i];
        for (int j = 0; j < w; j++)
            if (board[i][j] == 'C')
                site.push_back({i, j});
    }
    tie(sr, sc) = site[0];
    tie(er, ec) = site[1];

    fill(&dist[0][0][0], &dist[0][0][0] + 20000, INF);
    dist[sr][sc][0] = dist[sr][sc][1] = 0;
    deque<Tint> q{{sr, sc, 0}, {sr, sc, 1}};

    while (!q.empty()) {
        auto [cr, cc, mod] = q.front();
        q.pop_front();

        for (int k = 1-mod; k < 4; k += 2) {
            int nr = cr + adj[k][0], nc = cc + adj[k][1];
            if (nr < 0 || nr >= h || nc < 0 || nc >= w || board[nr][nc] == '*')
                continue;
            if (dist[nr][nc][mod] > dist[cr][cc][mod]) {
                dist[nr][nc][mod] = dist[cr][cc][mod];
                q.push_front({nr, nc, mod});
            }
        }

        if (dist[cr][cc][1-mod] > dist[cr][cc][mod] + 1) {
            dist[cr][cc][1-mod] = dist[cr][cc][mod] + 1;
            q.push_back({cr, cc, 1-mod});
        }
    }

    cout << min(dist[er][ec][0], dist[er][ec][1]);

    return 0;
}

Algorithm