밀집 그래프에서의 BFS

BFS의 다른 구현

다음 그래프에 대해 꼭짓점 A에서 시작하는 BFS를 고려해봅시다.

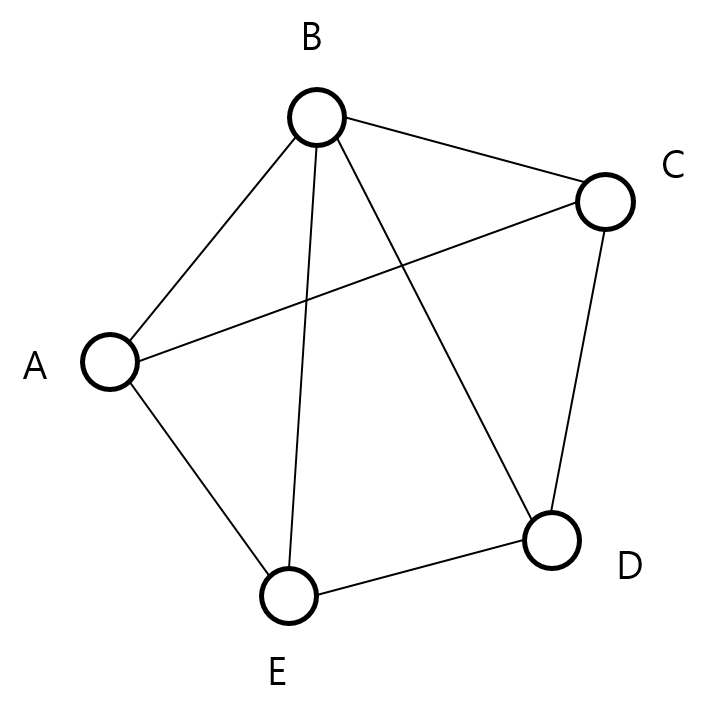
일단 A를 방문 처리하고 A까지 최단 거리를 0으로 둬야죠. 나머지는 거리 무한대고요. 그리고 큐에 A를 넣습니다.

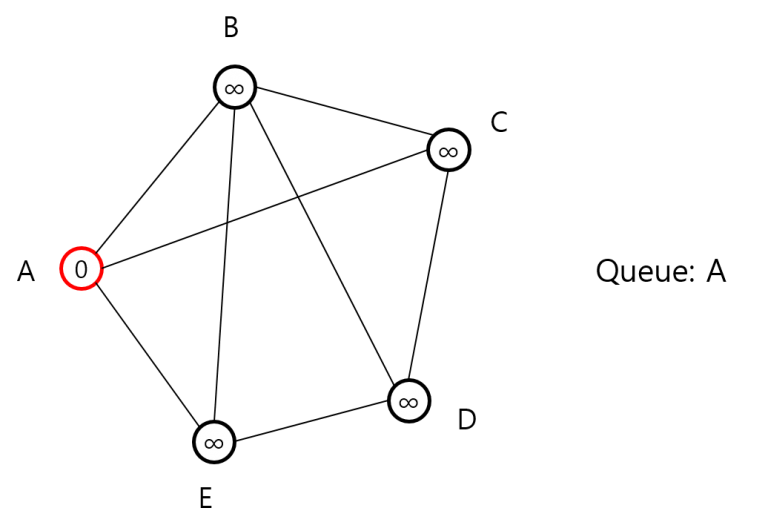
큐에서 제일 첫 원소 A를 빼낸 다음 A와 인접한 꼭짓점 중 방문하지 않은 것들의 거리를 업데이트하고 방문 처리하고 큐에 넣어줍니다.

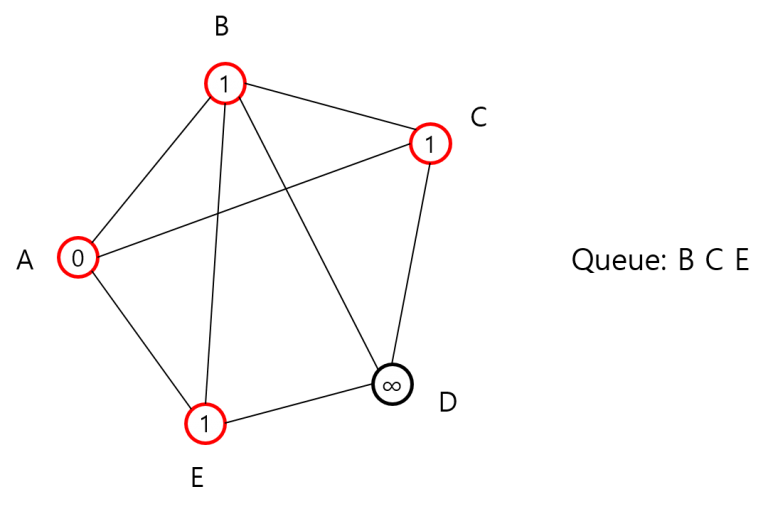
그 다음 큐에서 B를 꺼내고 B와 인접한 꼭짓점 A, C, D, E를 보게 될 텐데 생각해보니 굳이 인접한 꼭짓점을 다 봐야 할까요? 어차피 B, C, E는 이미 방문했는데, 이것까지 보는 건 낭비 같습니다. 그렇다면 아직 방문하지 않은 꼭짓점들의 집합을 두고 여기에 해당하는 것만 보면 되지 않을까요? 다시 처음부터 가서, 이번엔 아직 방문하지 않은 꼭짓점의 집합 Unvisited를 두고 시작합니다.

처음 시작은 아래와 같습니다.

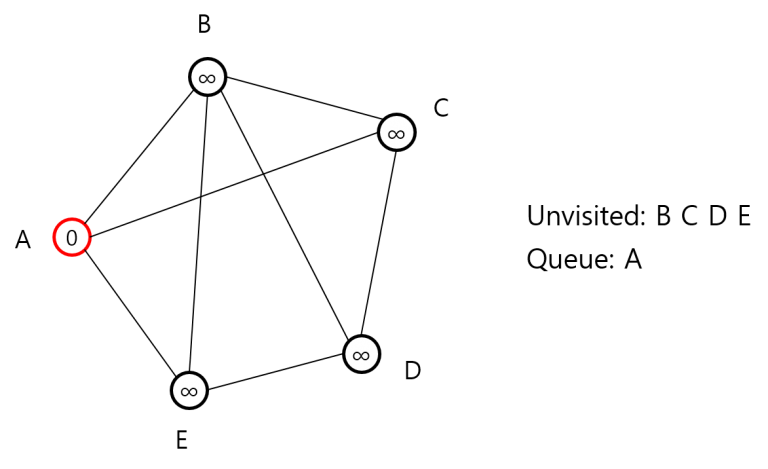
이제 Unvisited에서 B, C, D, E 각각을 보면서 A와 인접했을 경우 거리를 업데이트하고 Unvisited에서 뺀 뒤 큐에 넣습니다.

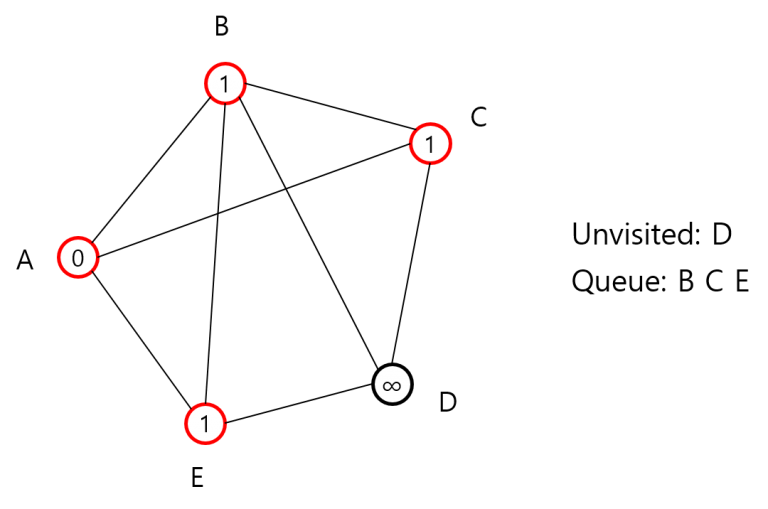
Unvisited에는 D만 있고, B와 D는 인접하므로 D를 거리 업데이트 후 Unvisited에서 빼면서 BFS는 종료됩니다.

보시다시피 방문 처리를 어떻게 하는가 외에는 일반적인 BFS와 아무런 차이가 없습니다. 대신 시간복잡도는 조금 다르겠죠. 일반적인 BFS는 각 꼭짓점은 정확히 한 번 거리 업데이트와 방문 처리 및 큐 삽입/삭제가 일어나고 각 꼭짓점에 대해 그와 인접한 꼭짓점을 탐색하므로 인접 꼭짓점 탐색 횟수는 정확히 변의 개수의 두 배입니다. 따라서 시간 복잡도가 $O(|V|+|E|)$죠.

반면에 이 BFS는 각 꼭짓점에 대해 인접한 꼭짓점 말고 Unvisited 집합에 있는 꼭짓점을 탐색합니다. 따라서 각 꼭짓점이 탐색되는 횟수는 언제 그 꼭짓점이 Unvisited에서 빠져나오냐에 달렸습니다. 다섯 번째 꼭짓점을 방문하고 나서 해당 꼭짓점이 Unvisited에서 빠져나오면 그 다섯 꼭짓점을 방문할 때마다 그 꼭짓점이 탐색이 되니 탐색 횟수는 5번이겠죠. Unvisited에서 빠지려면 인접한 꼭짓점을 방문해야 하므로 최악의 경우는 인접하지 않은 꼭짓점을 모두 방문하고 해당 꼭짓점을 방문하는 겁니다. 따라서 꼭짓점 $v$가 탐색되는 최대 횟수는 $|V|-1-\deg(v)$입니다.

꼭짓점을 하나 탐색할 때마다 둘 사이에 변이 있는지 탐색해야 하는데, 이걸 이분 탐색으로 처리한다고 하면 꼭짓점 하나 탐색하는 데 걸리는 시간은 $O(\log|V|)$입니다. 그러면 탐색에 걸리는 시간은 총

또는 완전 그래프 $K_{|V|}$에서 빠진 변의 개수를 $M$이라 하면

이므로 위 식은 $O(M\log|V|)$로도 쓸 수 있습니다. 또 모든 꼭짓점은 정확히 한 번 Unvisited에서 빠지는데 이걸 set으로 구현하면 여기 걸리는 시간은 총 $O(|V|\log|V|)$입니다. 따라서 최종 시간복잡도는 $O((|V|+M)\log|V|)$가 됩니다. $M$이 충분히 작은 밀집 그래프에서는 일반적인 BFS가 $O(|V|+|E|)=O(|V|^2)$만큼 걸리는 걸 생각하면 이쪽이 훨씬 빠르죠.

응용

BOJ 9264:: Intercity

문제를 요약하자면, 꼭짓점이 $N$개 있는 완전 그래프(꼭짓점은 1번부터 $N$번까지)에서 $K$개의 변은 가중치가 $A$이고 나머지는 가중치가 $B$일 때 1번 꼭짓점에서 $N$번 꼭짓점으로 가는 최단거리를 구하는 문제입니다. 만약 꼭짓점 1과 $N$ 사이 변의 가중치가 $A$라면 이걸 타거나 아니면 둘러가는 경로를 타야 할텐데 이 경로가 가중치 $A$인 변을 통과하면 무조건 더 긴 경로죠. 그러므로 가중치 $B$인 변만 통과하는 우회 경로를 찾아서 길이를 구하고 이를 $A$와 비교해서 작은 쪽을 골라야 합니다. 1과 $N$ 사이 변의 가중치가 $B$일 때도 마찬가지가 성립하므로 결론적으로 이 문제는 1부터 $N$까지 가중치 $A$인 변만 지나거나 $B$인 변만 지나는 최단 거리를 구하는 문제가 됩니다. 가중치 $A$인 변만 지나는 최단 경로는 일반적인 BFS로 구할 수 있고, $B$인 변만 지나는 최단 경로는 이 글에서 설명한 BFS로 구할 수 있습니다.

#include <bits/stdc++.h>

using namespace std;

using ll = long long;
using ull = unsigned long long;
using Pint = pair<int, int>;
using Tint = tuple<int, int, int>;

int n, k, a, b, u, v;
vector<int> adj[500000];

constexpr int INF = 1000000000;

int bfs_sparse(void) {
    queue<int> q;
    vector<bool> visited(n, false);

    q.push(0);
    visited[0] = true;

    int lv = 0;
    while (!q.empty()) {
        int sz = q.size();
        while (sz--) {
            int cur = q.front();
            q.pop();
            if (cur == n - 1)
                return lv;
            for (int nxt : adj[cur])
                if (!visited[nxt]) {
                    visited[nxt] = true;
                    q.push(nxt);
                }
        }
        lv++;
    }
    return INF;
}

int bfs_dense(void) {
    queue<int> q;
    set<int> unvisited;
    vector<int> dist(n, INF);

    q.push(0);
    for (int i = 1; i < n; i++)
        unvisited.insert(i);
    dist[0] = 0;

    while (!q.empty()) {
        int cur = q.front();
        q.pop();
        for (auto it = unvisited.begin(); it != unvisited.end();) {
            if (!binary_search(adj[cur].begin(), adj[cur].end(), *it)) {
                dist[*it] = dist[cur] + 1;
                q.push(*it);
                it = unvisited.erase(it);
            }
            else
                it++;
        }
    }
    return dist[n - 1];
}

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n >> k >> a >> b;
    for (int i = 0; i < k; i++){
        cin >> u >> v;
        adj[u - 1].push_back(v - 1);
        adj[v - 1].push_back(u - 1);
    }

    for (int i = 0; i < n; i++)
        sort(adj[i].begin(), adj[i].end());

    cout << min((long long)bfs_sparse() * a, (long long)bfs_dense() * b);

    return 0;
}