순환
공간 상에 놓인 폐곡선 $\mathcal{C}$에 대해 순환(circulation)을 다음과 같이 정의합니다.
\[ \Gamma = \oint\limits_\mathcal{C} \V\cdot\ud\mathbf{l} \]
적분 방향은 출처마다 다르지만 2차원의 경우엔 시계 방향이 훨씬 편합니다(그래서 정의에 음의 부호를 붙이는 사람도 있습니다). 폐곡선 $\mathcal{C}$를 경계로 하는 곡면 $D$를 생각하면 스토크스 정리에 의해 순환을 아래와 같은 방식으로도 쓸 수 있습니다.
\[ \Gamma = \iint\limits_D (\nabla\times\V)\cdot\mathbf n\mathrm dS \]
켈빈의 순환 정리
폐곡선 $\mathcal{C}$가 유체와 같이 흘러간다고 하면 $\mathcal{C}$ 상에서 순환은 어떻게 바뀔까요? 순환의 물질 도함수를 계산해봅시다.
\[
\frac{\uD\Gamma}{\uD t}
= \frac{\uD}{\uD t}\oint\limits_\mathcal{C} \V\cdot\ud\mathbf l
= \oint\limits_\mathcal{C} \frac{\uD\V}{\uD t}\cdot\ud\mathbf l + \oint_\limits{\mathcal{C}} \V\cdot\frac{\uD\ud\mathbf l}{\uD t}
\]
$\mathcal{C}$가 시간에 따라 달라지므로 $\ud\mathbf{l}$도 시간의 함수임에 유의합시다. 속도의 물질 도함수는 나비에-스토크스 방정식에 의하여 계산할 수 있습니다.
\[ \frac{\uD\V}{\uD t} = \mathbf{g}-\frac{1}{\rho}\nabla p+\frac{\mu}{\rho}\nabla^2\V+\frac{\mu+\lambda}{\rho}\nabla(\nabla\cdot\V) \]
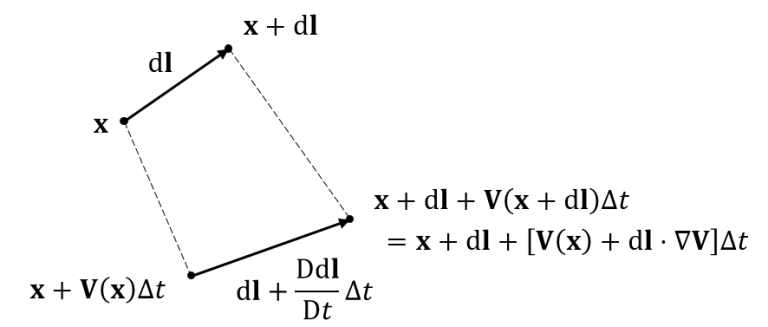
그리고 $\uD\ud\mathbf{l}/\uD t$는 아래 그림에서
\begin{gather}
\ud\mathbf l+\frac{\uD\ud\mathbf l}{\uD t}\Delta t = \left\{\x+\ud\mathbf l+[\V(\x)+\ud\mathbf l\cdot\nabla\V]\Delta t\right\}-\left\{\x+\V(\x)\Delta t\right\} =\ud\mathbf l+\ud\mathbf l\cdot\nabla\V\Delta t \nonumber \\
\therefore \frac{\uD\ud\mathbf l}{\ud t} = \ud\mathbf l\cdot\nabla\V
\end{gather}
따라서 순환의 물질 도함수는
\begin{equation}
\frac{\uD\Gamma}{\uD t}
= \oint\limits_\mathcal{C} \left[\mathbf g-\frac{1}{\rho}\nabla p+\frac{\mu}{\rho}\nabla^2\V+\frac{\mu+\lambda}{\rho}\nabla(\nabla\cdot\V)\right]\cdot\ud\mathbf l
+ \oint\limits_\mathcal{C} \V\cdot(\ud\mathbf l\cdot\nabla\V)
\label{eq:circ-matderiv}
\end{equation}
여기서 세 가지 가정을 도입해봅시다.
비점성 유동
밀도가 압력만의 함수이런 유체를 순압 유체(barotropic fluid)라고 합니다. 공기는 순압 유체가 아니지만(밀도가 온도와 압력의 함수) 비압축성으로 가정하면 밀도가 상수이므로 순압 유체입니다.
체적력이 모두 보존력
일단 식 \eqref{eq:circ-matderiv}에서 점성항을 모두 없앱시다.
\begin{equation*}
\frac{\uD\Gamma}{\uD t}
= \oint\limits_\mathcal{C} \mathbf{g}\cdot\ud\mathbf{l}
- \oint\limits_\mathcal{C} \frac{1}{\rho}\nabla p\cdot\ud\mathbf{l}
+ \oint\limits_\mathcal{C} \V\cdot(\ud\mathbf{l}\cdot\nabla\V)
\end{equation*}
폐곡선을 따라 보존력이 한 일은 0이므로 첫 번째 항은 0입니다. 스토크스 정리를 써서 두 번째 항을 면적분으로 바꾸고 세 번째 항을 약간 정리하면
\begin{align*}
\frac{\uD\Gamma}{\uD t}
&= -\iint\limits_D \nabla\times\left(\frac{1}{\rho}\nabla p\right)\cdot\ud\mathbf{l}
+ \frac12 \cancel{\oint\limits_\mathcal{C} \nabla\left(V^2\right)\cdot\ud\mathbf{l}} \\
&= -\iint\limits_D \left( \frac{1}{\rho}\cancel{\nabla\times\nabla p} + \nabla\frac{1}{\rho}\times\nabla p \right) \cdot\ud\mathbf{l} \\
&= \iint\limits_D \frac{1}{\rho^2}(\nabla\rho\times\nabla p)\cdot\ud\mathbf{l}
\end{align*}
$\nabla\rho$는 등밀도면의 법선 벡터이고 $\nabla p$는 등압면의 법선 벡터인데 밀도가 압력만의 함수이므로 등밀도면은 등압면과 일치하고 따라서 둘은 나란합니다. 결과적으로 위 세 가지 가정 하에서 순환의 물질 도함수는
\[ \frac{\uD\Gamma}{\uD t} = 0 \]
즉, 보존력만이 작용할 때 순압 비점성 유동에서는 순환이 보존됩니다. 이를 켈빈의 순환 정리(Kelvin’s circulation theorem)라고 합니다.
왜 퍼텐셜 유동인가
위에서 설명했듯이 비압축성 유체는 순압 유체이므로 유체역학에서 다루는 유동 중 가장 간단한 외력이 없는 비압축성, 비점성 유동은 켈빈의 순환 정리를 만족해야 합니다. 여기서 만약 유입 유동이 속도가 일정한 균일 유동(uniform flow)이라면 그 순환은 항상 0이므로 켈빈의 순환 정리에 의해 유동 어디에서든 어떤 폐곡선을 생각하더라도 순환이 0입니다. 따라서 모든 점에서 와도가 0이어야 하고, 결국 이 유동은 퍼텐셜 유동입니다.
물론 현실의 유동은 거의 모두 점성 유동이지만, 퍼텐셜 유동을 가정하여도 꽤나 그럴듯하게 유동을 모사할 수 있습니다. 이때 점성에 의한 효과는 경계층 이론 등을 이용해 계산하게 됩니다.