유선 함수
비압축성 유동에서 연속 방정식은
\[ \nabla\cdot\V = 0 \]
여기서 유동이 2차원 평면 유동이라 하고 평면 상에 고정된 폐곡선 $\mathcal{C}$와 그 내부 영역 $D$를 생각합시다. 연속 방정식을 $D$ 위에서 적분하면 발산 정리에 의해
\[ \iint\limits_D (\nabla\cdot\V) \ud\mathcal{S} = \int\limits_C \V\cdot\mathbf n\ud\mathcal{l} = 0 \]
여기서 $\mathbf n$은 $D$의 바깥쪽을 향하는 단위 법선 벡터입니다. 이 식은 $\mathcal{C}$를 통과하는 (단위 깊이당) 알짜 부피 유량이 항상 0이라는 걸 의미합니다.
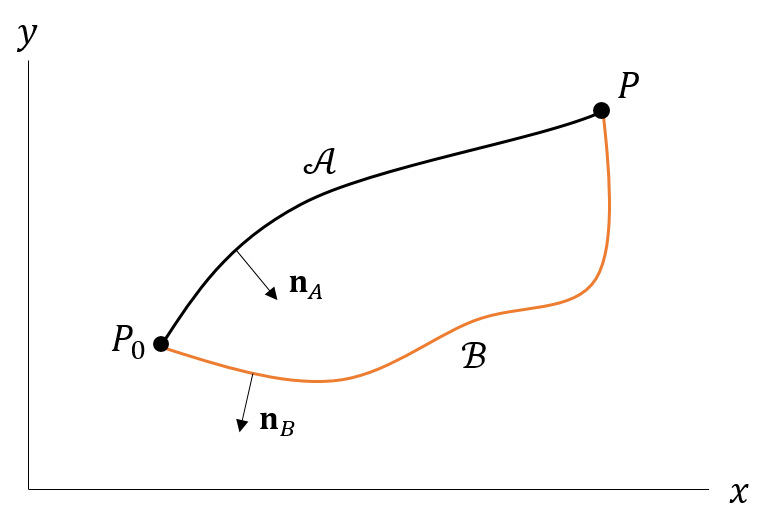
이제 점 $P_0$에서 다른 점 $P$를 잇는 두 곡선 $\mathcal{A}$와 $\mathcal{B}$를 생각해봅시다. $\mathcal{A}$와 $\mathcal{B}$를 합하면 폐곡선이 되므로 위 식에 따라
\begin{gather}
\int_\limits{\mathcal{A}}\V\cdot(-\mathbf n_A)\ud\mathcal{l} + \int_\limits{\mathcal{B}}\V\cdot\mathbf n_B\ud\mathcal{l} = 0 \nonumber \\
\therefore \int_\limits{\mathcal{A}}\V\cdot\mathbf n_A\ud\mathcal{l} = \int_\limits{\mathcal{B}}\V\cdot\mathbf n_B\ud\mathcal{l}
\end{gather}
즉, $\mathcal{A}$를 통과하는 부피 유량과 $\mathcal{B}$를 통과하는 부피 유량은 동일합니다. 두 점 사이를 지나는 부피 유량은 적분 경로를 어떻게 잡든 상관 없다는 말이죠. 그러니, 최대한 간단하게 축에 평행하게 잡아버립시다.
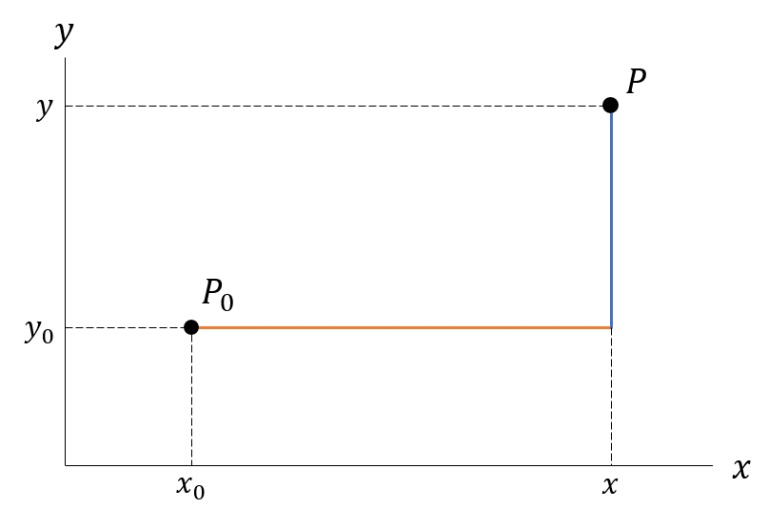
이때 $P_0$와 $P$ 사이를 지나는 부피 유량은
\[ \int_{x_0}^x \V\cdot(0, -1)\ud x + \int_{y_0}^y\V\cdot(1, 0)\ud y = -\int_{x_0}^x v(x’, y_0)\ud x’ + \int_{y_0}^y u(x, y’)\ud y’ \]
이 값은 $P$에 따라 달라지므로 $x$와 $y$의 함수로 쓸 수 있습니다.
\[ \psi(x, y) = -\int_{x_0}^x v(x’, y_0)\ud x’ + \int_{y_0}^y u(x, y’)\ud y’ \]
기준점 $P_0$에서는 함숫값이 0입니다. 한편 위 함수를 $y$에 대해 편미분하면 첫째 항은 $x$만의 함수이므로
\[ \frac{\rd\psi}{\rd y} = u(x,y) \]
한편 적분 경로를 다음과 같이 잡으면
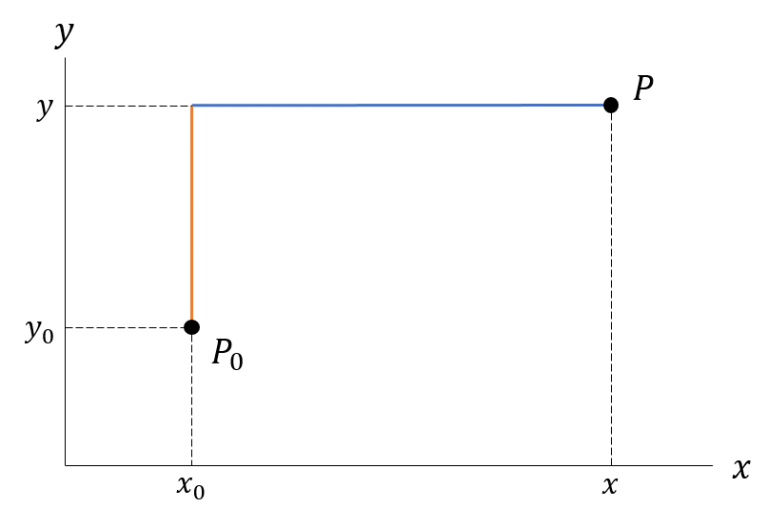
비슷한 방법으로 $x$에 대한 편미분을 얻습니다.
\[ \frac{\rd\psi}{\rd x} = -v(x,y) \]
따라서 2차원 유동의 경우 속도장을 함수 하나의 편도함수로 나타낼 수 있습니다.
\[ \V = \left( \frac{\rd\psi}{\rd y}, -\frac{\rd\psi}{\rd x} \right) \]
실제로 이걸 연속 방정식 $\nabla\cdot\V=0$에 대입하면 성립합니다. 또한 함수에 상수를 더하더라도 여전히 동일한 유동을 나타냅니다. 상수를 더한다는 건 단순히 함수값이 0이 되는 기준점 $P_0$를 다르게 둔다는 의미이기 때문입니다.
만약 기준점이 아닌 두 점 사이의 부피 유량은 어떻게 될까요?
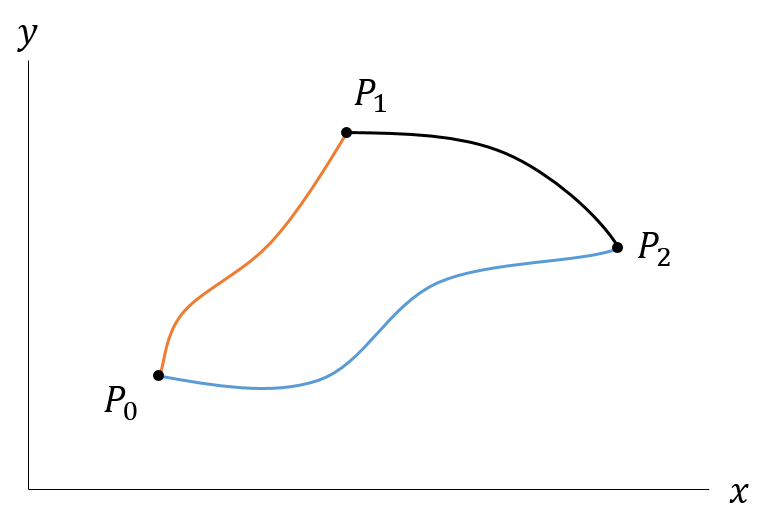
$P_1$과 $P_2$ 사이를 지나는 부피 유량은 $P_0$와 $P_2$ 사이 부피 유량에서 $P_0$와 $P_1$ 사이 부피 유량을 뺀 값입니다. 그러므로 $\psi(P_2)-\psi(P_1)$이 됩니다. 즉, 두 점 사이를 지나는 부피 유량은 함숫값의 차이와 같습니다.
여기서 두 점이 같은 유선 위에 있다면 속도 벡터는 절대 유선을 통과하지 않아 유선을 통과하는 부피 유량이 0이기 때문에 함숫값이 동일합니다. 따라서 함수 $\psi$의 등고선이 곧 유선이 됩니다. 이러한 이유로 $\psi$는 유선 함수(stream function)라고 부릅니다.
다음 2차원 비압축성 유동에 대해 유선 함수와 점 $(1,1)$을 지나는 유선의 방정식을 구해봅시다.
\begin{equation*} \V = (-2x, 2y + 1) \end{equation*}
유선 함수의 편도함수를 적분합니다.
\begin{align*} \frac{\partial\psi}{\partial x} &= -v = -2y-1 &&\Rightarrow & \psi &= -2xy-x+f(y) \\ \frac{\partial\psi}{\partial y} &= u = -2x &&\Rightarrow & \psi &= -2xy+g(x) \end{align*}
\begin{equation*} \therefore \psi = -2xy-x+c \end{equation*}
여기서 $c$는 임의의 상수이며 보통 0으로 두거나 특정 점에서 0이 되도록 정합니다. 점 $(1,1)$을 지나는 유선의 방정식은 그 점에서 유선 함수의 값이 $c-3$이므로 다음과 같습니다.
\begin{equation*} -2xy-x = -3 \end{equation*}
스토크스 유선 함수
축대칭(axisymmetric) 유동은 2차원 유동과 유사하기 때문에 유선 함수 비슷한 것을 정의할 수 있습니다. 대칭축을 포함하는 한 단면 상의 두 점 $P_0$와 $P$를 연결하는 곡선 $\mathcal{C}$를 생각합시다. 이때 $\mathcal{C}$를 대칭축을 중심으로 한 바퀴 회전하여 만들어지는 곡면을 통과하는 부피 유량은 비압축성 유동의 경우에 $\mathcal{C}$에 상관없이 동일합니다. 그 부피 유량
\begin{equation*} \int_\limits{\mathcal{C}} 2\pi r \V\cdot\mathbf{n} \ud\mathcal{l} \end{equation*}
을 $2\pi$로 나눈 값을 스토크스 유선 함수(Stokes stream function)이라 부르고 흔히 $\Psi$로 표기합니다.
\[ \Psi = \int_\limits{\mathcal{C}} r\V\cdot\mathbf{n} \ud\mathcal{l} \]
원통 좌표계

$\mathcal{C}_1$을 따라 적분하면
\begin{gather}
\Psi = -\int_{r_0}^r r’u_z(r’,z_0)\mathrm dr’+\int_{z_0}^z ru_r(r,z’)\mathrm dz’ \nonumber \\
\therefore \frac{\rd\Psi}{\rd z} = ru_r(r,z)
\end{gather}
$\mathcal{C}_2$를 따라 적분하면
\begin{gather}
\Psi = \int_{z_0}^z r_0u_r(r_0,z’)\mathrm dz’-\int_{r_0}^r r’u_z(r’,z)\mathrm dr’ \nonumber \\
\therefore \frac{\rd\Psi}{\rd r} = -ru_z(r,z)
\end{gather}
구면 좌표계

$\mathcal{C}_1$을 따라 적분하면
\begin{gather}
\Psi = -\int_{\theta_0}^\theta r_0\sin\theta’ u_r(r_0, \theta’)\cdot r_0\mathrm d\theta’ +\int_{r_0}^r r’\sin\theta u_\theta(r’, \theta)\mathrm dr’ \nonumber \\
\therefore \frac{\rd\Psi}{\rd r} = r\sin\theta u_\theta(r,\theta)
\end{gather}
$\mathcal{C}_2$를 따라 적분하면
\begin{gather}
\Psi = \int_{r_0}^r r’\sin\theta_0 u_\theta(r’, \theta_0)\mathrm dr’ -\int_{\theta_0}^\theta r\sin\theta’ u_r(r, \theta’)\cdot r\mathrm d\theta’ \nonumber \\
\therefore \frac{\rd\Psi}{\rd \theta} = -r^2\sin\theta u_r(r,\theta)
\end{gather}
유선 함수의 부호에 관하여
부피 유량을 계산할 때 법선 벡터의 방향을 반대로 잡으면 유선 함수의 부호가 반대가 됩니다. 물론 여전히 연속 방정식을 만족하므로 문제는 없지만, 문헌에 따라 유선 함수의 부호를 다르게 쓰는 경우가 많아 주의해야 합니다.
속도 퍼텐셜
속도장의 회전, 즉 와도가 0인 유동을 비회전 유동(irrotational flow)이라고 합니다. 회전이 0인 벡터장은 어떤 스칼라 함수의 기울기로 쓸 수 있으므로,
\[ \V = \nabla\phi = \left(\frac{\partial\phi}{\partial x}, \frac{\partial\phi}{\partial y}, \frac{\partial\phi}{\partial z}\right) \]
이때 함수 $\phi$를 속도 퍼텐셜(velocity potential)이라고 합니다. 유선 함수와 마찬가지로 속도 퍼텐셜에 어떤 상수가 더해져도 동일한 유동을 나타냅니다. 또, 유선 함수의 값이 일정한 점들을 모은 곡선이 유선이 되듯이 속도 퍼텐셜이 일정한 면은 등퍼텐셜면(equipotential surface)이라고 합니다.
비회전 유동은 속도 퍼텐셜이 존재한다는 점에서 퍼텐셜 유동(potential flow)이라고도 부릅니다.
다음 퍼텐셜 유동에 대해 속도 퍼텐셜과 점 $(2,0,1)$을 지나는 등퍼텐셜면의
방정식을 구하여라.
\begin{equation*} \V = (2xy, x^2, 1) \end{equation*}
정의에 의해
\begin{align*}
\frac{\partial\phi}{\partial x}&=2xy &&\Rightarrow &\phi&=x^2y + f(y, z) \\
\frac{\partial\phi}{\partial y}&=x^2 &&\Rightarrow &\phi&=x^2y + g(z, x) \\
\frac{\partial\phi}{\partial z}&=1 &&\Rightarrow &\phi&=z + h(x, y)
\end{align*}
\begin{equation*} \therefore \phi = x^2y + z + c \end{equation*}
점 $(2,0,1)$을 지나는 등퍼텐셜면은
\begin{equation*} x^2y + z = 1 \end{equation*}
퍼텐셜 유동은 얼핏 보면 인위적인 가정 같지만 물리적으로는 타당한 가정입니다. 물리적 의미는 다음 글에서 설명하겠습니다.
유선과 등퍼텐셜선의 관계
2차원 비압축성 퍼텐셜 유동은 유선 함수와 속도 퍼텐셜이 모두 정의되고, 따라서 유선과 등퍼텐셜선(2차원이니까 면 대신 선)을 생각할 수 있습니다. 이 둘의 관계는 어떻게 될까요?
기울기의 성질에 의해 $\nabla\psi$는 유선에 수직하고 $\nabla\phi$는 등퍼텐셜선에 수직합니다. 그런데
\[ \nabla\psi\cdot\nabla\phi=\frac{\partial\psi}{\partial x}\frac{\partial\phi}{\partial x} +\frac{\partial\psi}{\partial y}\frac{\partial\phi}{\partial y}=(-v)u+uv=0 \]
이므로 유선과 등퍼텐셜선은 수직합니다.





